Lid-driven cavity#
The lid-driven cavity flow is a incompressible viscous flow.
In 2-dimensions, it is usually cast as follows. The domain is set to be
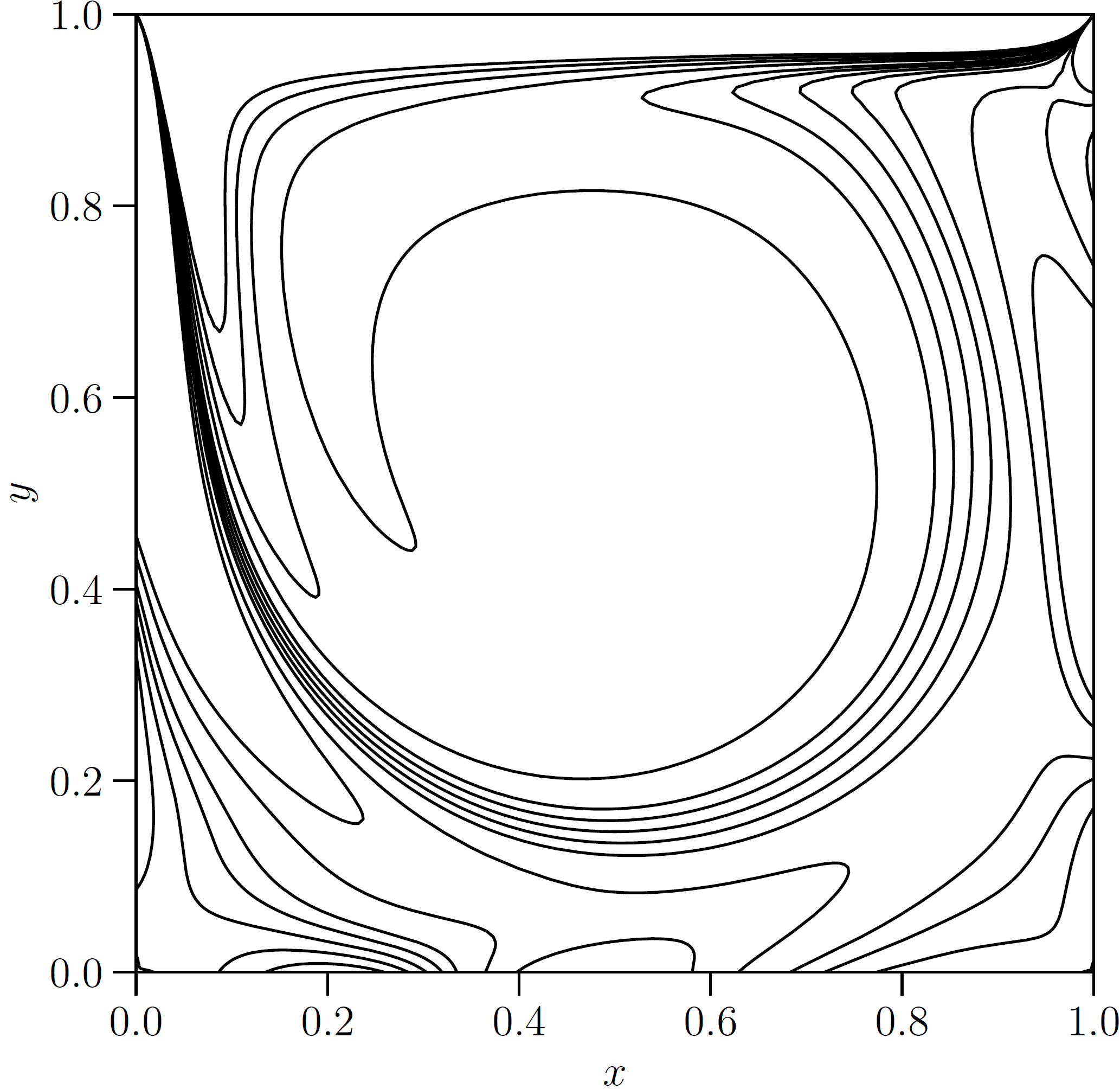
Fig. 12 The steady case of
For a phyem implementation of the normal dipole collision test case in Section 5.4 of
[MEEVC, Zhang et al., JCP (2024)], click
phyem_ldc.py.
↩️ Back to 🌊 Navier-Stokes equations.

