Cylinder channel

The cylinder channel is a mesh (or domain) in \(\mathbb{R}^n\), \(n\in\left\lbrace2,3\right\rbrace\). The 2d domain is illustrated in the following figure.

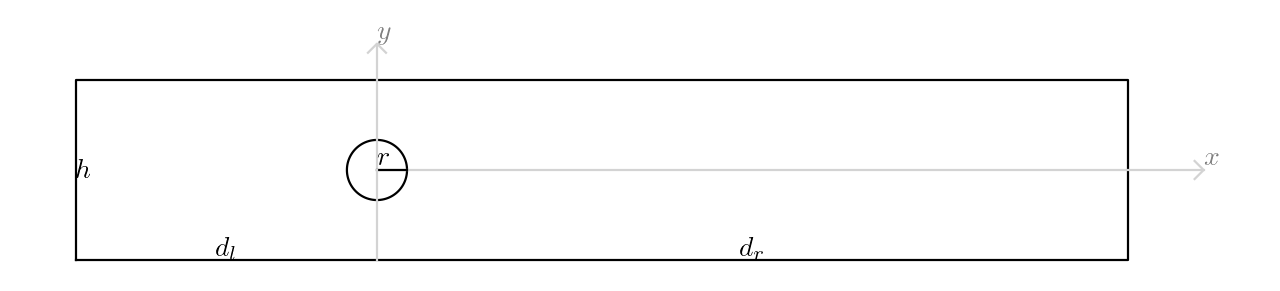
Fig. 6 The illustration of the 2d cylinder channel domain.

cylinder_channel(r=1, dl=8, dr=25, h=6, w=0, periodic=True)

Parameters:

rfloat, default=1

The radius of the cylinder.

dlfloat, default=8

The \(x\) distance from the left boundary to the cylinder center.

drfloat, default=25

The \(x\) distance from the right boundary to the cylinder center.

hfloat, default=6

The height (along \(y\)-direction, \([-h/2, h/2]\)) of the channel; must have \(h/2 > r\).

wfloat, default=0

The width (along \(z\)-direction, \([-w/2, w/2]\)) of the channel.

periodicbool, default=True

When the domain is 3d, whether it is periodic along the \(z\)-axis? It has no affect when w=0 (the domain is 2d).

Boundary units

The cylinder channel domain is divided into 7 regions. The topology of these regions is illusrated in the following figure.

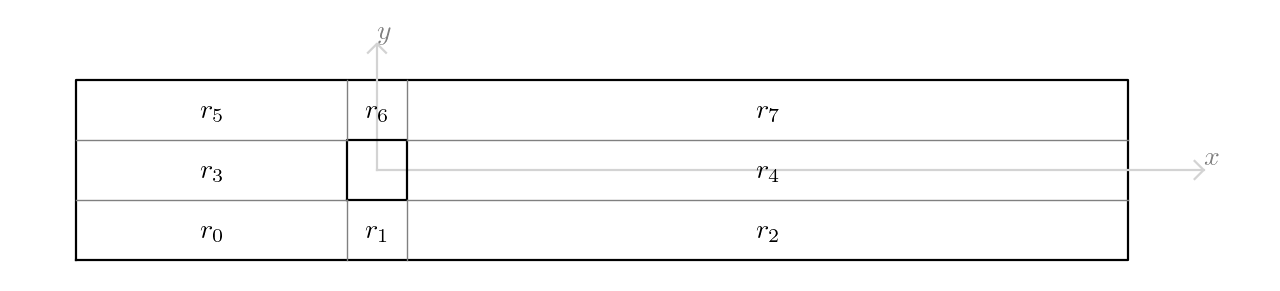
Fig. 7 The illustration of the topology of regions in a 2d cylinder channel domain.

Thus, the complete set of boundary units in 2 dimensions is

>>> boundary_units_set = {
...     0: [1, 0, 1, 0],
...     1: [0, 0, 1, 1],
...     2: [0, 1, 1, 0],
...     3: [1, 1, 0, 0],
...     4: [1, 1, 0, 0],
...     5: [1, 0, 0, 1],
...     6: [0, 0, 1, 1],
...     7: [0, 1, 0, 1],
... }

And, for example, if we call the left side the inlet, we can pick up boundary units for the inlet by

>>> boundary_units_inlet = {
...     0: [1, 0, 0, 0],
...     3: [1, 0, 0, 0],
...     5: [1, 0, 0, 0]
... }

The cylinder surface is

>>> boundary_units_inlet = {
...     1: [0, 0, 0, 1],
...     3: [0, 1, 0, 0],
...     4: [1, 0, 0, 0],
...     6: [0, 0, 1, 0]
... }

Examples

2d

We can generate a mesh in this domain by doing

>>> ph.config.set_embedding_space_dim(2)
>>> manifold = ph.manifold(2)
>>> mesh = ph.mesh(manifold)
>>> msepy, obj = ph.fem.apply('msepy', locals())
>>> manifold = obj['manifold']
>>> mesh = obj['mesh']
>>> msepy.config(manifold)('cylinder_channel')
>>> msepy.config(mesh)(3)  # refining factor, a positive integer.
>>> mesh.visualize(saveto=None_or_custom_path)  
<Figure size ...

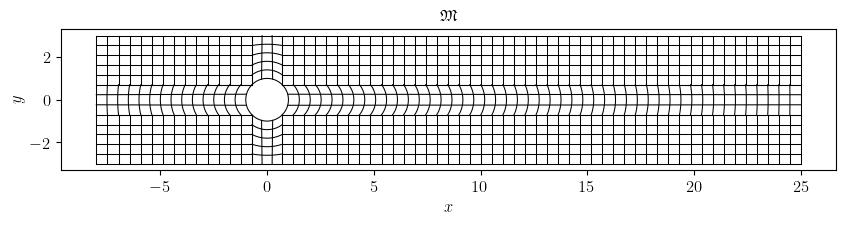
Fig. 8 The cylinder_channel mesh of element factor 3.

Note that we configure the mesh with a factor 3. Increasing this factor to refine the mesh.