Multi-crazy domain and mesh#
The multi-crazy ones are like stacking multiple Crazy domain and mesh
(blocks) together. The parameters are same to those of the crazy
mesh except there is one additional, Ns, see:
- crazy_multi(bounds=None, c=0, Ns=None, periodic=False)[source]#
- Parameters:
- boundslist, tuple,
None, default=None The bounds of the domain along each axis. When it is
None, the code will automatically analyze the manifold and set theboundsto beFor example, the unit cube is of
bounds = ([0, 1], [0, 1], [0, 1]).- cfloat, default=0.
The deformation factor.
cmust be inc = 0, the domain is orthogonal, and whenc > 0, the space in the domain is distorted.- Nslist, None, default=None
Nsshould be a list ofWhen it is
None, the code will automatically analyze the manifold and then setNsto be- periodicbool, default=False
It indicates whether the domain is periodic. When it is
True, the domain is fully periodic along all axes. And when it isFalse, the domain is not periodic at all.
- boundslist, tuple,
Boundary units#
Since the amount of regions is dynamic, its amount of boundary units is dynamic as well.
They contain the boundary faces of these regions attached to the domain boundary. For example, when
there are
>>> boundary_units_set = {
... 0: [1, 0, 1, 0],
... 1: [0, 1, 1, 0],
... 2: [1, 0, 0, 0],
... 3: [0, 1, 0, 0],
... 4: [1, 0, 0, 1],
... 5: [0, 1, 0, 1],
... }
Examples#
We now generate a multi-crazy mesh in domain
>>> ph.config.set_embedding_space_dim(2)
>>> manifold = ph.manifold(2)
>>> mesh = ph.mesh(manifold)
>>> msepy, obj = ph.fem.apply('msepy', locals())
>>> manifold = obj['manifold']
>>> mesh = obj['mesh']
>>> msepy.config(manifold)('crazy_multi', c=0.3, periodic=False, Ns=[2, 3], bounds=[[-1, 1], [0, 2]])
>>> msepy.config(mesh)([5, 3])
>>> mesh.visualize(saveto=None_or_custom_path)
<Figure size ...
The multi-crazy mesh is visualized as
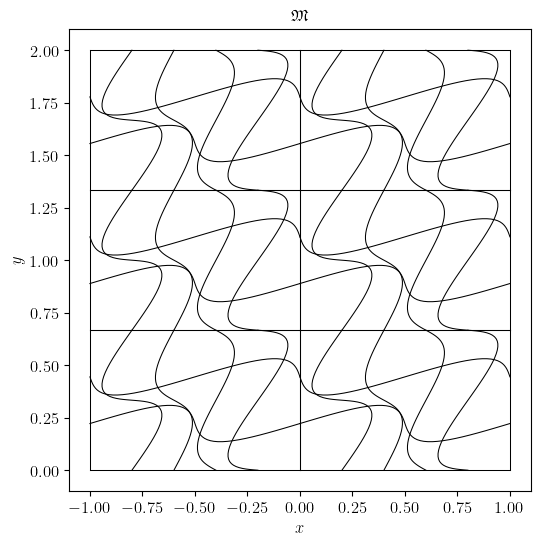
Fig. 9 The crazy mesh in
↩️ Back to msepy domains and meshes.

